FIR (Finite impulse response) filter
Overview
Finite impulse response (FIR) filters are characterized by the fact that they use only delayed versions of the input signal to filter the input to the output.
For a causal discrete-time FIR filter of order N, each value of the output sequence is a weighted sum of the most recent input values:
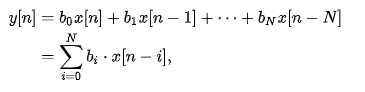
Where:
- x[n] is the input signal,
- y[n] is the output signal,
- N is the filter order
- bi is the value of the impulse response, also a coefficient of the filter
Filter design
FIR filter designing is finding the coefficients and filter order that meet certain specifications. When a particular frequency response is desired, several different design methods are common:
- Window design method
- Frequency sampling method
- Least MSE (mean square error) method
- Parks-McClellan method
- DFT algorithms
There many software such as MATLAB, GNU Octave, Scilab and SciPy (Python).
In this topic, I only share how to implement FIR filter on FPGA. So the detail of filter designing, finding coefficients will shared in the later topics.
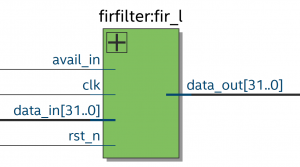
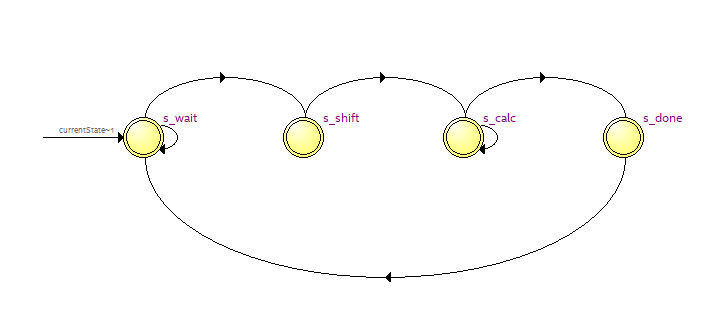
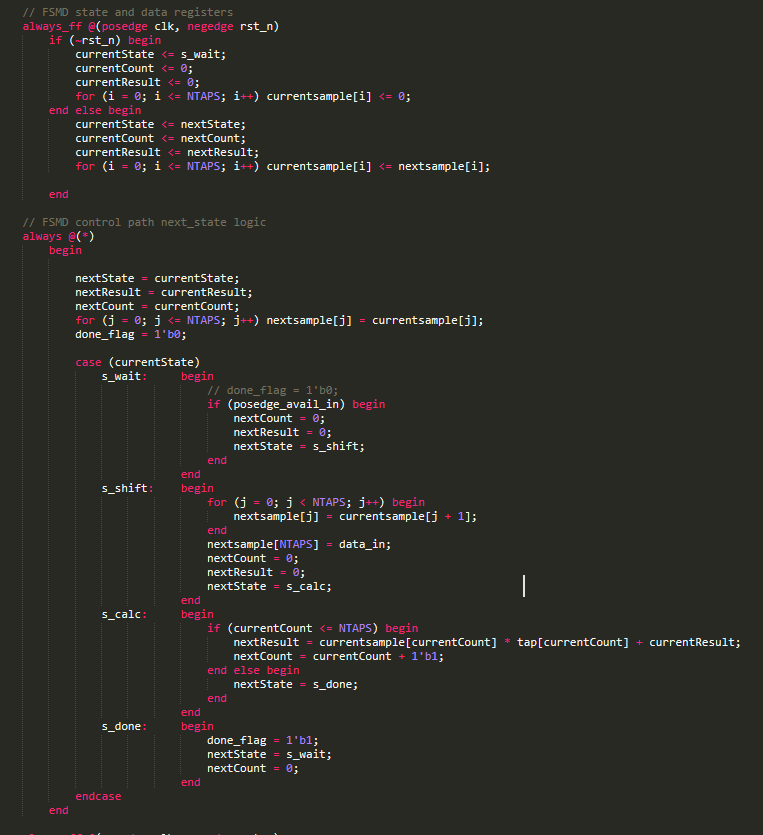
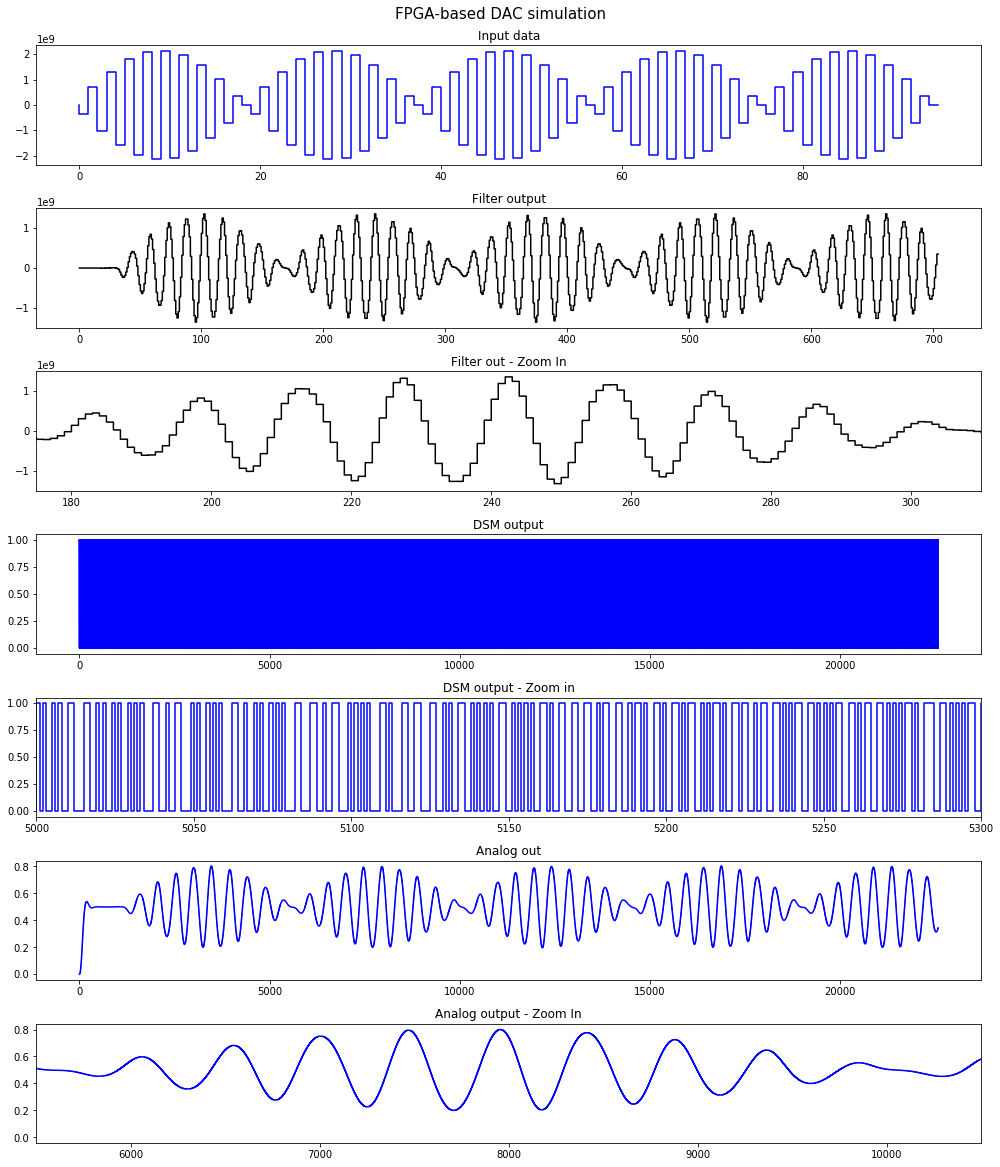
Implementing a FIR filter on FPGA for slow signal
FIR filter for slow signal will designed by using special way to save the number of multipliers.
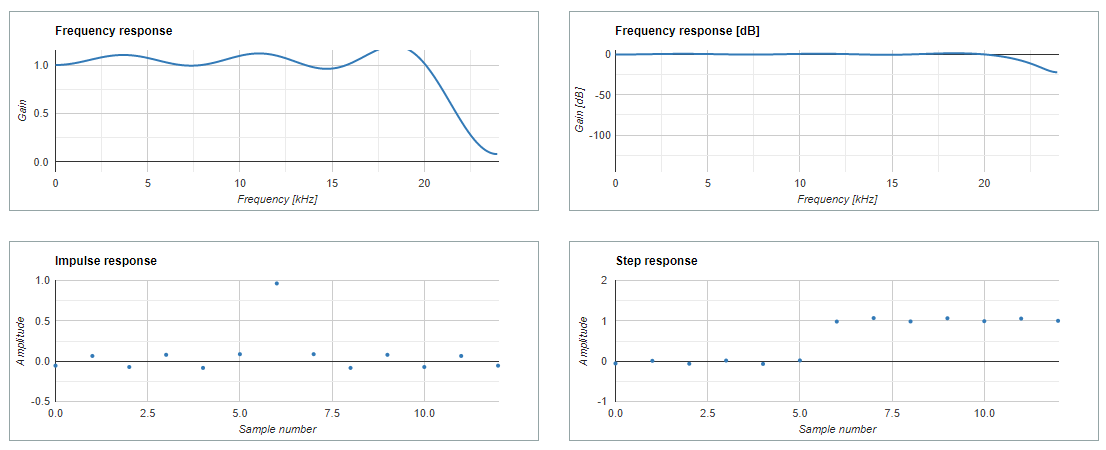
- Finding coefficients using window method
Using Python
from future import print_function
from future import division
import numpy as np
fS = 48000 # Sampling rate.
fL = 22000 # Cutoff frequency.
N = 13 # Filter length, must be odd.
h = np.sinc(2 * fL / fS * (np.arange(N) – (N – 1) / 2))
h /= np.sum(h)
print(h)

2. Implementing on FPGA